第35回ツール・ド・おきなわ2023 – 熱帯の花となれ風となれ – 市民レース140kmマスターズ 17位
兄貴です。毎年シーズン最後を飾るツール・ド・おきなわに今年も参戦してきた。今年は市民レース ...

まえばし赤城山ヒルクライム大会 2023 一般男子C 優勝
兄貴です。どん底からの復活。というのがふさわしいほど自信を失いかけていたが、レースの結果は ...

第11回榛名山ヒルクライム in 高崎 男子C(40歳以上~49歳以下)29位
兄貴です。 実は昨年末に第一子が誕生し、育児に仕事にという状況で参加するか相当悩み、結局エ ...

ツール・ド・おきなわ 2022 市民レース100km(マスターズ) 無念のパンク27位
兄貴です。 2019年以来、新型コロナウイルスの影響で開催が見送られていたツール・ド・おき ...
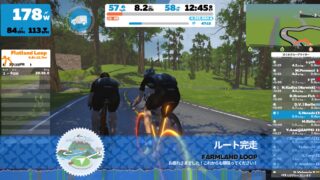
2022/1/12 Wed. – Zwift Haute Route Nation Rides // Steady Pace (B) からの Never Not Riding By Specialized Asia (D)
兄貴です。ベースライドにちょうどよさそうな、キットアンロックのあるイベントがあったので走っ ...
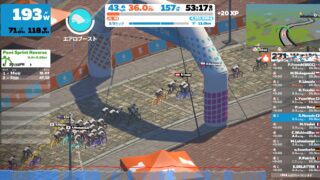
2022/1/11 Tue. – Zwift TdZ Stage 1: Long Ride
兄貴です。Tour de Zwift の季節がまた今年もやってきたということで、さっそく ...

2022/1/10 Mon. – Zwift Watopia Ride with B. Brevet
兄貴です。出たいイベントも特になかったので、ペースパートナー (B) を試すことにした。 ...

2022/1/9 Sun. – Zwift EVO CC Fat Burn/Steady State (2-5 -2.6wkg avg)からのHotchillee Ride Sunday Endurance Series (C)
兄貴です。日曜日だし今日もベースライドということで、適当そうなイベントをチョイスしてみ ...
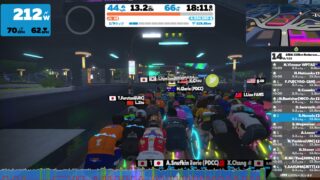
2022/1/8 Sat. – Zwift ASIA 130km Endurance Ride (B)
兄貴です。最近、日本のZwifterに人気の(?)毎週土曜日朝8:00からやっている、AS ...
2022/1/7 Fri. – Zwift Fast Fridays: Bologna Time Trial からの Ride with C Cadence
兄貴です。久々に刺激を入れようと Zwift で TT を走ることにした。 エントリーした ...